Machine learning (ML) has great potential for improving products and services across various industries. However, the explainability of ML models is crucial for their widespread adoption. First, explanation helps build trust and transparency between the users and the models. When users understand how ML model works, they are more likely to trust its results. Moreover, explainability allows for better debugging of complex models. By providing explanations for models’ decisions, researchers can gain insights into the underlying patterns, which helps identify potential biases or flaws. Furthermore, the explainability of models enables auditing, a prerequisite for its usage in regulated industries, such as finance and healthcare.
To benefit from an explainable model, we introduced permutation feature importance as a global explanation method to SAP HANA Predictive Analysis Library (PAL) in the past several months. In this blog post, we will show how to use it in Python machine learning client for SAP HANA (hana-ml), which provides a friendly Python API for many algorithms from PAL.
After reading this blog post, you will learn:
◉ Permutation feature importance from its theory to usage
◉ Two alternative global explanation methods available and their comparison to permutation feature importance
Permutation feature importance
Permutation feature importance is a feature evaluation method that measures the decrease in the model score when we randomly shuffle the feature's values. It reveals the extent to which a specific feature contributes to the overall predictive power of the model by breaking the association between the feature and the true outcome.
Behind the screen the permutation importance is calculated in the following steps:
i. Initially, a reference score is evaluated on the original dataset.
ii. Next, a new dataset is generated by permuting the column of a specific feature, and the score is evaluated again.
iii. Then the permutation importance is defined as the difference between the reference score and the score obtained from permuted dataset.
By repeating the second and third steps for each feature, we can get the importance scores for the entire dataset.
Permutation importance provides highly compressed, global insight to gauge the relative importance of each feature, enabling data scientists and analysts to prioritize their efforts on the most influential variables when building and optimizing models. This approach is particularly useful for handling high-dimensional datasets, as it helps identify the most informative features amidst a vast number of possible predictors.
Here we use the well-known Titanic dataset to illustrate the usage of permutation importance. In hana-ml, there is a class called DataSets that offers various public datasets. To load the dataset, we can utilize the load_titanic_data method.
from hana_ml import dataframe
from hana_ml.algorithms.pal.utility import DataSets
conn = dataframe.ConnectionContext(url, port, user, pwd)
titanic_full, _, _, _ = DataSets.load_titanic_data(conn)
Titanic dataset describes the survival status of individual passengers on the RMS Titanic. The objective is to predict based on passenger data (i.e. name, age, gender, socio-economic class, etc.) whether a passenger can survive the shipwreck. In our dataset we have 12 columns, and the meaning of each column is below:
- PassengerId - Unique ID assigned to each passenger.
- Pclass - Class of ticket purchased (1 = 1st class, 2 = 2nd class, 3 = 3rd class).
- Name - Full name and title of the passenger.
- **bleep** - Gender of the passenger.
- Age - The Age of the passenger in years.
- SibSp - Number of siblings and spouses associated with the passenger aboard.
- Parch - Number of parents and children associated with the passenger aboard.
- Ticket - Ticket number.
- Fare - The fare of the ticket purchased by the passenger.
- Cabin - The Cabin number that the passenger was assigned to. If NaN, this means they had no cabin and perhaps had not assigned one due to the cost of their ticket.
- Embarked - Port of embarkation (S = Southampton, C = Cherbourg, Q = Queenstown).
- Survived - Survival flag of passenger (0 = No, 1 = Yes), target variable.
To keep things simple and stay on track with our example, we will remove columns with a high number of null values and then build a predictive model to forecast survival status using the remaining features. We rely on PAL's built-in support in classification algorithm for handling other data preprocessing issues like missing values and dataset splitting.
from hana_ml.algorithms.pal.unified_classification import UnifiedClassification
rdt_params = dict(n_estimators=100,
max_depth=56,
min_samples_leaf=1,
split_threshold=1e-5,
random_state=1,
sample_fraction=1.0)
uc_rdt = UnifiedClassification(func = 'RandomDecisionTree', **rdt_params)
features = ["PCLASS", "NAME", "**bleep**", "AGE", "SIBSP", "PARCH", "FARE", "EMBARKED"]
uc_rdt.fit(data=titanic_full, key='PASSENGER_ID', features=features, label='SURVIVED',
partition_method='stratified', stratified_column='SURVIVED', partition_random_state=1,
training_percent=0.7, output_partition_result=True,
ntiles=2, categorical_variable=['PCLASS','SURVIVED'], build_report=False,
permutation_importance=True, permutation_evaluation_metric='accuracy',
permutation_n_repeats=10, permutation_seed=1, permutation_n_samples=None)
RandomDecisionTree has a practical method for estimating missing data. When it comes to training data, the method calculates the median of all values for numerical variable or the most frequent non-missing value for categorical variable in a certain class, and then uses that value to replace all missing values of that variable within that class. As for test data, the class label is absent, so one missing value is replicated for each class and filled with the corresponding class’s median or most frequent item.
UnifiedClassification has a method for dataset splitting, so we can use it to randomly split our dataset, using 70% for training and leaving the rest for validating. In addition, RandomDecisionTree has built-in support for categorical variables; all we need to do is specify the parameter categorical_variable for variables that come in integer type.
To enable the calculation of permutation feature importance, set permutation_importance to True. Additionally, use permutation_evaluation_metric to define the evaluation metric for importance calculation. For classification problems, options include accuracy, auc, kappa and mcc, while for regression problems, options are RMSE, MAE and MAPE. Set permutation_n_repeats to specify the number of times a feature is randomly shuffled. Because shuffling the feature introduces randomness, the results might vary greatly when the permutation is repeated. Averaging the importance measures over repetitions stabilizes the measure at the expense of increased computation time. Use permutation_seed to set the seed for randomly permuting a feature column, which ensures reproducible results across function calls. Moreover, set permutation_n_samples to determine the number of samples to draw in each repeat. While this option may result in less accurate importance estimates, it helps manage computational speed when evaluating feature importance on large datasets. By combining permutation_n_samples with permutation_n_repeats, we can control the trade-off between computational speed and statistical accuracy of this method.
Permutation importance does not indicate the inherent predictive value of a feature but how important this feature is for a specific model. It is possible that features considered less important for a poorly performing model (with a low cross-validation score) could actually be highly significant for a well-performing model. Therefore it is crucial to assess the predictive power of a model using a held-out set prior to determining importances.
uc_rdt.statistics_.collect()
| STAT_NAME | STAT_VALUE | CLASS_NAME |
| AUC | 0.7385321100917431 | None |
| RECALL | 0.9674418604651163 | 0 |
| PRECISION | 0.7247386759581882 | 0 |
| F1_SCORE | 0.8286852589641435 | 0 |
| SUPPORT | 215 | 0 |
| RECALL | 0.29464285714285715 | 1 |
| PRECISION | 0.825 | 1 |
| F1_SCORE | 0.43421052631578944 | 1 |
| SUPPORT | 112 | 1 |
| ACCURACY | 0.7370030581039755 | None |
| KAPPA | 0.3097879442371883 | None |
| MCC | 0.37957621849462986 | None |
We can check the model performance on validation set directly from fitted attribute statistics_. Its validation performance, measured via the accuracy score, is significantly larger than the chance level. This makes it possible to use permutation importance to probe the most predictive features.
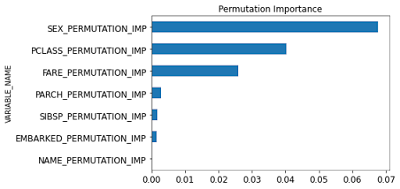
import matplotlib.pyplot as plt
df_imp = uc_rdt.importance_.filter('IMPORTANCE >= 0').collect()
df_imp = df_imp.sort_values(by=['IMPORTANCE'], ascending=True)
c_title = "Permutation Importance"
df_imp.plot(kind='barh', x='VARIABLE_NAME', y='IMPORTANCE', title=c_title, legend=False, fontsize=12)
plt.show()
Feature importances are provided by the fitted attribute importances_. We can visually represent the feature contributions using a bar chart.
While there is some element of luck involved in surviving, it seems some groups of people were more likely to survive than others. The most important features for predicting survival status with a random forest are **bleep**, Pclass and fare, whereas passenger’s family relations or name are deemed less important.
This is reasonable because women were given priority access to the lifeboats, so they were more likely to survive. Also, both Pclass and fare can be regarded as a proxy for socio-economic status (SES). People with higher SES may have had better access to information, resources, and connections to secure a spot on a lifeboat or be rescued more quickly. They may also possess more experience with navigating emergency situations and better access to survival skills and knowledge.
Compared to gender and SES, factors such as port of embarkation, family relations, or name played a limited role in survival. Because the chaotic and rapidly evolving nature of the sinking meant that all passengers were subject to the same evacuation protocols, these factors were less relevant in determining a passenger's likelihood of survival.
Apart from permutation feature importance, there are two additional techniques existing in PAL can be used to gain a global explanation. One is impurity-based feature importance computed on tree-based models and another is SHAP feature importance obtained by aggregating local Shapley values for individual predictions. We will delve into these methods individually through the subsequent two case studies.
Case Study: impurity-based feature importance
Tree-based models provide an alternative measure of feature importance deriving from nodes’ splitting process.
Individual decision trees intrinsically perform feature selection by selecting appropriate split points. This information can be used to measure the importance of each feature; the basic idea is if a feature is frequently used in split points, it is considered more important. In practice, importance is calculated for a single decision tree by evaluating how much each attribute split point improves performance, weighted by the number of observations under each node. The performance measure may be the purity used to select the split points or another more specific error function.
This notion of importance can be extended to decision tree ensembles by simply averaging the impurity-based feature importance of each tree. By averaging the estimates over several randomized trees, the variance of the estimate is reduced, making it suitable for feature selection. This is known as the mean decrease in impurity, or MDI.
Note that this computation of feature importance is based on the splitting criterion of the decision trees (such as Gini index), and it is distinct from permutation importance which is based on permutation of the features.
We show the calculation of impurity-based importance on Titanic dataset. The calculation is incorporated in the fitting of RandomDecisionTree, as demonstrated in the code below.
from hana_ml.algorithms.pal.unified_classification import UnifiedClassification
rdt_params = dict(n_estimators=100,
max_depth=56,
min_samples_leaf=1,
split_threshold=1e-5,
random_state=1,
sample_fraction=1.0)
uc_rdt = UnifiedClassification(func = 'RandomDecisionTree', **rdt_params)
features = ["PCLASS", "NAME", "**bleep**", "AGE", "SIBSP", "PARCH", "FARE", "EMBARKED"]
uc_rdt.fit(data=titanic_full, key='PASSENGER_ID', features=features, label='SURVIVED',
partition_method='stratified', stratified_column='SURVIVED', partition_random_state=1,
training_percent=0.7, output_partition_result=True,
ntiles=2, categorical_variable=['PCLASS','SURVIVED'], build_report=False
)
uc_rdt.statistics_.collect()
Prior to inspecting feature importance, it is important to ensure that the model predictive performance is high enough. Indeed, there is no point in analyzing the important features of a non-predictive model. Here we can observe that the validation accuracy is high, indicating that the model can generalize well thanks to the built-in bagging of random forests.
The feature importance scores of a fitted model can be accessed via the importance_ property. This dataframe has rows representing each feature, with positive values that add up to 1.0. Higher values indicate a greater contribution of the feature to the prediction function.
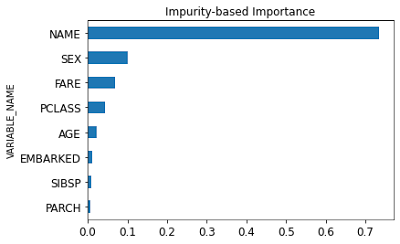
import matplotlib.pyplot as plt
df_imp = uc_rdt.importance_.collect()
df_imp = df_imp.sort_values(by=['IMPORTANCE'], ascending=True)
c_title = "Impurity-based Importance"
df_imp.plot(kind='barh', x='VARIABLE_NAME', y='IMPORTANCE', title=c_title, legend=False, fontsize=12)
plt.show()
A bar chart is plotted to visualize the feature contributions.
Oops! The non-predictive passenger’s name is ranked most important by the impurity-based method which contradicts the permutation method. However, the conclusions regarding the importance of the other features still hold true. The same three features are detected most important by both methods, although their relative importance may vary. The remaining features are less predictive.
So, the only question is why impurity-based feature importance assigns high importance to variables that are not correlated with the target variable (survived).
This stems from two limitations of impurity-based feature importance. First, impurity-based importance can inflate the importance of high cardinality features, that is features with many unique values (such as passenger’s name). Furthermore, impurity-based importance suffers from being computed on training set statistics and it cannot be evaluated on a separate set, therefore it may not reflect a feature’s usefulness for make predictions that generalize to unseen data (if the model has the capacity to use the feature for overfit).
The fact that we use training set statistics explains why passenger’s name has a non-null importance. And the bias towards high cardinality features explains further why the importance has such a large value.
As shown in previous example, permutation feature importance does not suffer from the flaws of the impurity-based feature importance: it does not exhibit a bias toward high-cardinality features and can be computed on a left-out validation set (as we do in PAL). Using a held-out set makes it possible to identify the features that contribute the most to the generalization power of the inspected model. Features that are important on the training set but not on the held-out set might cause the model to overfit. Another key advantage of permutation feature importance is that it is model-agnostic, i.e. it can be used to analyze any model class, not just tree-based models.
However, the computation for full permutation importance is more costly. There are situations that impurity-based importance is preferable. For example, if all features are numeric and we are only interested in representing the information acquired from the training set, limitations of impurity-based importance don’t matter. If these conditions are not met, permutation importance is recommended instead.
Now that we have completed our exploration of impurity-based importance, let's shift our focus to SHAP feature importance.
Case Study: SHAP feature importance
SHAP (SHapley Additive exPlanations) is a technique used to explain machine learning models. It has its foundations in coalitional game theory, specifically Shapley values. These values determine the contribution of each player in a coalition game. In the case of machine learning, the game is the prediction for a single instance, features act as players, and they collectively contribute to the model’s prediction outcome. SHAP assigns each feature a Shapley value and uses these values to explain the prediction made by the model.
The SHAP calculation can be invoked in the prediction method of UnifiedClassification. Once again, we show its application on Titanic dataset. The RandomDecisionTree model is trained as before. To ensure a more valid comparison to permutation importance, we deliberately employ SHAP on the validation set.
uc_rdt.partition_.set_index("PASSENGER_ID")
titanic_full.set_index("PASSENGER_ID")
df_full = uc_rdt.partition_.join(titanic_full)
features = ["PCLASS", "NAME", "**bleep**", "AGE", "SIBSP", "PARCH", "FARE", "EMBARKED"]
pred_res = uc_rdt.predict(data=df_full.filter('TYPE = 2'), key='PASSENGER_ID', features=features, verbose=False,
missing_replacement='feature_marginalized',
top_k_attributions=10, attribution_method='tree-shap')
pred_res.select("PASSENGER_ID", "SCORE", "REASON_CODE").head(5).collect()
SHAP by itself is a local explanation method explains the predictions for individual instances. Since we run SHAP for every instance, we get a matrix of Shapley values. This matrix has one row per data instance and one column per feature. To get a global explanation, we need a rule to combine these Shapley values.
In practice, there are different ways to aggregate local explanations. For instance, we can assess feature importance by analyzing how frequently a feature appears among the top K features in the explanation or by calculating the average ranking for each feature in the explanation. In our case, we opt to use mean absolute Shapley values as an indicator of importance.
The idea behind this is simple: Features with large absolute Shapley values are considered important. Since we want the global importance, we average the absolute Shapley values for each feature across the data. We can then arrange the features in descending order of importance and present them in a plot, like what we have done before. Another simpler solution is to utilize the ShapleyExplainer module as a visualizer and let it handle the task.
from hana_ml.visualizers.shap import ShapleyExplainer
features=["PCLASS", "NAME", "**bleep**", "AGE", "SIBSP", "PARCH", "FARE", "EMBARKED"]
shapley_explainer = ShapleyExplainer(feature_data=df_full.filter('TYPE = 2').select(features),
reason_code_data=pred_res.select('REASON_CODE'))
shapley_explainer.summary_plot()
There is a big difference between SHAP feature importance and permutation feature importance. Permutation feature importance is based on the decrease in model performance, while SHAP is based on magnitude of feature attributions. In other words, SHAP feature importance reflects how much the model’s prediction varies can be explained by a feature without considering its impact on performance. If changing a feature greatly changes the output, then it is considered important. As a result, SHAP importance gives higher importance to features that cause high variation in the prediction function.
Although model variance explained by the features and feature importance are strongly correlated when the model generalizes well (i.e. it does not overfit), this distinction becomes evident in cases where a model overfits. If a model overfits and includes irrelevant features (like the passenger’s name in this instance), the permutation feature importance would assign an importance of zero because this feature does not contribute to accurate predictions. SHAP importance measure, on the other hand, might assign high importance to the feature as the prediction can change significantly when the feature is altered.
Additionally, it is noteworthy that calculating SHAP can be computationally demanding, especially for models that are not based on trees. If you are only looking for a global explanation, it is suggested to use permutation importance.

No comments:
Post a Comment